





Introduction to the Personnel module:
Introduction to the Payroll module:
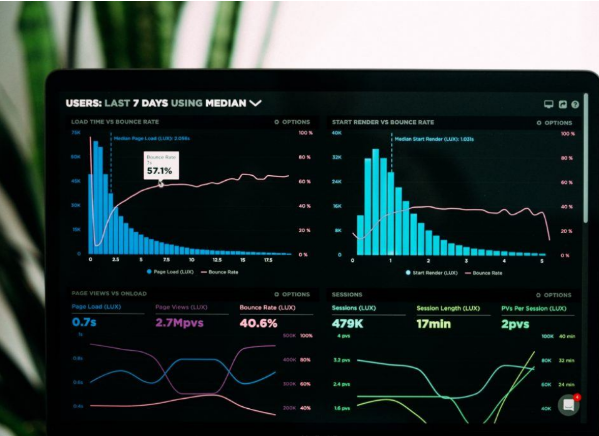
Representing data using graphics such as tables, diagrams, infographics, heat maps, bubble clouds, scatter plots, and mekko charts is called data visualization. These visual displays and information representations help communicate complex data relationships and data-driven insights in a way that makes it easy to understand and inform decisions.
The goal of data visualization is to help identify patterns and trends from large data sets. Data refers to the processing of immersive and interactive visualizations that show new data as it is streamed. There is a huge volume of data available today, and to gain any benefit from that abundance of data, real-time analytics has become extremely necessary for businesses to gain an edge over their competition. Real-time visualizations can be very useful for companies that need to make strategic or on-the-fly decisions.
It is useful for companies that need to deal with risk, both managing it and responding if something goes wrong. And, for those companies that can use these real-time visualizations to take advantage of emerging opportunities before someone else does. Real-time visualizations work best when input-based action needs to be taken immediately by providing context to decision makers.
Business benefits of data visualization:
Information processing: With a constant stream of data being generated in real time, it is impossible to process and make sense of it just by looking at it. Visualization helps make sense of the clutter of numbers and text in a better way. It is also easier to absorb and interpret data when it is presented visually.
Relevant insights: Data visualization provides relevant insights by connecting and showing patterns of how different data sets are connected. This can help easily identify and extract trends and patterns that might not otherwise be visible from the raw data. This is especially important when streaming data is presented and trends can be forecast using real-time visualizations.
In financial trading systems, such real-time data visualizations can show real-time ROI, profit and loss and help companies make immediate decisions.
Business operations: Data visualizations give businesses insight overview of the current relationship between various sections and operations of the business. help in the decision-making process and in the management of critical business metrics. Can Help review and analyze areas for improvement.
Decision making: The pattern becomes clearer with data visualization, facilitating faster decision making. Since there is a synchronization between real-time data and its visualization, companies can make quick decisions that can significantly affect the organization.
Customer Analytics: Real-time data visualization helps analyze customer data to understand business trend. It can reveal information about the understanding and knowledge of the target audience, their preferences and more. Such insights can be helpful in designing strategies that can address customer requirements.
Save time: It is easier to understand, process and make decisions based on graphically represented data instead of going through tons of reports with raw data and generate reports on time. Real-time data visualizations help save time by categorizing and displaying trends and patterns in real time.
Data Interaction: Data visualization helps group and categorize data and encourages employees to spend time on data interaction through data visualization. This leads to better ideas and helps in problem solving. Help design and create actionable business solutions.
Real-time data visualization provides additional context for decision makers who need to respond immediately when faced with risk, and for businesses that need to make quick decisions before an opportunity is missed.
Some of the use cases for real-time data visualizations are:
Conclusion
Data is the key to decision making in any business. Helping the decision-making process by actively rendering real-time data using different real-time rendering and visualization methods can give the business a winning competitive advantage.
This website uses cookies to optimize your browsing experience, improve performance, analyze traffic, and personalize content. You can accept all cookies or manage your preferences at any time.
